Una funció és una relació entre dos conjunts numèrics (habitualment, subconjunts de $ℝ$), que associa un únic nombre del segon conjunt a cada element i, per tant, nombre del primer conjunt. El primer conjunt es denomina domini de la funció, i el segon, imatge o recorregut de la funció. Per a reconèixer una funció, acostuma a designar-se per una o algunes lletres de l’alfabet. Per exemple, si la funció $f$ entre dos conjunts numèrics associa l'element 3 del domini de $f$ $\left(\text{o}\mathrm{Dom}\left(f\right)\right)$ l'element $\mathrm{-7}$ de la imatge de $f$  $\left(\text{o}\mathrm{Im}\left(f\right)\right)$, pot expressar-se així:

$f(\underset{\underset{\begin{array}{l}\text{element}\\ \text{del}\\ \text{domini}\end{array}}{\uparrow }}{3})=\underset{\underset{\begin{array}{l}\text{element}\\ \text{de la}\\ \text{imatge}\end{array}}{\uparrow }}{-7}$

És útil conèixer certes eines que ajuden a treballar amb funcions:

• La taula d'una funció

Una taula d'una funció és una taula amb dues columnes; la primera compta valors del domini de la funció, i la segona els valors corresponents de la seva imatge. Per exemple, aquesta és una taula d'una funció $F$, de manera que $F\left(2\right)=1$, $F\left(4\right)=6$, $F\left(6\right)=3$, $F\left(8\right)=1$ i $F\left(41\right)=5$.

• L'expressió d'una funció

L'expressió d'una funció és una expressió algebraica amb una variable que permet trobar la imatge de qualsevol element del domini de la funció. Per a aconseguir-ho s'ha de substituir la variable de l'expressió pel valor del domini. Per exemple, si la funció $g$ fa correspondre a un nombre el seu quadrat, l'expressió d'aquesta funció ha de ser:

$g\left(x\right)=x^2$

• La gràfica d'una funció

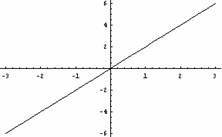
La gràfica d’una funció és el conjunt de tots els punts del pla cartesià $f\left(x\right)=y$ les coordenades del qual coincideixen amb els valors d’aquesta funció, de manera que la coordenada $x$ representa els valors del domini i la coordenada $y$ els valors de la imatge corresponent. Per a dibuixar la gràfica d'una funció, s'han de dibuixar tots els punts de la funció. Per exemple, aquesta és la gràfica de la funció $f\left(x\right)=2x$, el domini de la qual és l'interval$\left[-3,3\right]$.

• Operacions bàsiques entre funcions

Les operacions bàsiques entre funcions són la suma, la resta, la multiplicació, la divisió i la potenciació de funcions. Existeix també la composició de funcions: si f és una funció, i g és una altra funció, la funció composició de f amb g, $\mathrm{g\circ }f$ és defineix així: $\left(\mathrm{g\circ f}\right)\left(x\right)=g\left(f\right(x\left)\right)$. Per exemple, si f ( 3 ) = 5, i g ( 5 ) = − 3, llavors, ( g∘f ) ( 3 ) = g ( f ( 3 ) ) = g ( 5 ) = − 3. Es tracta, doncs, d'aplicar la funció g al resultat de la funció f.