Una funció a trossos (o per parts) és aquella que té diverses expressions per a cada part del domini.
Aquesta és la gràfica d’una funció definida a trossos, formada per una paràbola per a valors de menors que , i per una recta per a valors de majors o iguals que :
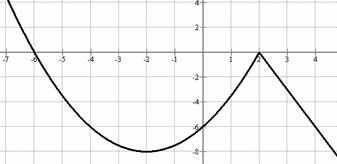
Troba
l'expressió algebraica de la funció.
Mostra/amaga la solució
Es tracta d'una
funció definida a trossos formada per una paràbola i una recta. Analitzem
primer la paràbola:
Passa pels punts
, , . A partir d'aquí pot plantejar-se un sistema
d'equacions i obtenir , i de l'expressió de la funció quadràtica
.
Ara bé, pot fer-se de manera més senzilla si s’utilitzen les arrels del polinomi associat. Una arrel del polinomi
és , i l'altra arrel és . Així, doncs, l'equació de la paràbola
és:
A més, sabem que
passa per ; per tant,
l'equació de la
paràbola és
Anem a buscar
l'equació de la recta que passa per i ; és del tipus
Restant ambdues
equacions queda
Així, doncs,
l'equació de la funció és:
