Una función es una relación entre dos conjuntos numéricos (habitualmente, subconjuntos de $ℝ$), que asocia un único número del segundo conjunto a cada elemento y, por lo tanto, número del primer conjunto. Al primer conjunto se le denomina dominio de la función y, al segundo, imagen o recorrido de la función. Para reconocer una función, suele nombrarse con una o algunas letras del alfabeto. Por ejemplo, si la función $f$ entre dos conjuntos numéricos, asocia el elemento $3$ del dominio de $f$ (o $\mathrm{Dom}\left(f\right)$) el elemento $\mathrm{-7}$ de la imagen de $f$ (o $\mathrm{Im}\left(f\right)$), puede expresarse así:

$f(\underset{\underset{\begin{array}{l}\text{elemento}\\ \text{del}\\ \text{dominio}\end{array}}{\uparrow }}{3})=\underset{\underset{\begin{array}{l}\text{elemento}\\ \text{de la}\\ \text{imagen}\end{array}}{\uparrow }}{-7}$

Es útil conocer ciertas herramientas que ayudan a trabajar con funciones:

• La tabla de una función

Una tabla de una función es una tabla con dos columnas; la primera contiene valores del dominio de la función y la segunda, los valores correspondientes de su imagen. Por ejemplo, ésta es una tabla de una función $F$, de manera que $F\left(2\right)=1$, $F\left(4\right)=6$, $F\left(6\right)=3$, $F\left(8\right)=1$ y $F\left(41\right)=5$.

• La expresión de una función

La expresión de una función es una expresión algebraica con una variable que permite encontrar la imagen de cualquier elemento del dominio de la función. Para conseguirlo, se debe sustituir la variable de la expresión por el valor del dominio. Por ejemplo, si la función $g$ hace corresponder a un número su cuadrado, la expresión de esta función debe ser:

$g\left(x\right)=x^2$

• La gráfica de una función

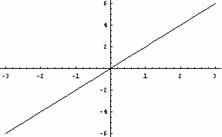
La gráfica de una función es el conjunto de todos los puntos del plano cartesiano $f\left(x\right)=y$ cuyas coordenadas coinciden con los valores de esta función, de manera que la coordenada $x$ representa los valores del dominio y la coordenada $y$ los valores de la imagen correspondiente. Para dibujar la gráfica de una función, se deben dibujar todos los puntos de la función. Por ejemplo, ésta es la gráfica de la función $f\left(x\right)=2x$ cuyo dominio es el intervalo $\left[-3,3\right]$.

• Operaciones básicas entre funciones

Las operaciones básicas entre funciones son la suma, resta, multiplicación, división y potenciación de funciones. Existe también la composición de funciones: si f es una función y g es otra función, la función composición de f con g, g∘ f se define así: ( g∘f ) ( x ) = g ( f ( x ) ). Por ejemplo, si f ( 3 ) = 5 y g ( 5 ) = − 3, entonces ( g∘f ) ( 3 ) = g ( f ( 3 ) ) = g ( 5 ) = − 3. Se trata, pues, de aplicar la función g al resultado de la función f.